Post by mareofnight on Mar 5, 2013 21:16:54 GMT
This discussion started in the "What are you thinking about right now?" thread on page 4 or so. I've split it off into its own thread in order to avoid driving everyone insane with math.
Here are the relevant posts (or at least most of them):

Well the consistent but minor effects are me getting headaches from being around full book shelves for more than a few hours, and checking the alarm clocks a lot before going to bed. And by a lot I mean in groups of 4 or 8....at 3 to 6 intervals. This latter effect really annoys my sister when we share the same bedroom. My extended family on both sides have their share of unusual mental thingummies and would probably be on TLC Hoarders if they didn't live in huge houses or own large amounts of land, so my immediate family just sort of let me have it, and even bought me a third alarm clock (although I only use two currently).

Yeah, It's pretty crazy. It's sort of because I learned statistics and if you check your alarm clock once, the probability of you not setting it correctly will go down. Naturally, if you check it a second time, the probability will go down even more. So assuming that checking one's alarm clock is independent, the probably of not setting it correctly is ~ 0. And 0 is where I need it to be, because I can't stand the thought of missing school or work because I dislike sleeping and will hence sleep in a lot if given the chance. ^^;;;;;;;
I like to think that I am a functioning human adult-ish people otherwise.

clemon re:alarms: Hmmm... So it's one of those L-shape graphs.

Would math help with this at all? Like... basically what's happening is either you value avoiding extremely small probabilities of setting your alarm wrong more highly than the time (and possibly annoyance) cost of checking it, or you're miscalculating expected utility of additional checking. I'll, umm... wait for you to say if you want me to explain this or not before I go into it in the interest of not being annoying |'D
 Re: Mental thingummy
Re: Mental thingummy
Math might work, although now it's sort of math + strange luck thingy; 4 is not really special to me, except from tvtropes I learned it's associated with "death" in Japan and it's a nice square number; and the only reason I check one clock 4 times in a row instead of 8 times for the other is because the 4-times-clock requires less buttons to check. I used to check it by going through the buttons until I didn't feel like I just started checking it (so basically consequently checking an alarm clock for 4 or 5 minutes straight). I sort of understand the probabilities like:
P(alarm not working with 1 check) = 0.50 for example, so assuming checks are independent (which they probably aren't) and the probability is .5 (kind of a over estimate of effects from lousy clock + human perception), then if I checked 1 clock only once, 1 out of every 2 days I would expect it not to work.
P(alarm not working with 2 checks) = 0.50^2 = 0.25 ...If I checked 1 clock twice, 1 of out of 4 days I would expect it not to work.
P(2 alarms not working with with 24 and 12 checks respectively) = 0.50^24 * 0.50^12 = 1.455 * 10 * -11 = 1.455/100,000,000,000 in about 273,972,602 years both clocks will fail once. So pretty much 0 right? The 12 and 24 checks are more by habit then by math now so hmmm...maybe I should lower the number of checks, but anyhow I am interested in your take on it.


@ My silly problem:
Yeah, It's pretty crazy. It's sort of because I learned statistics and if you check your alarm clock once, the probability of you not setting it correctly will go down. Naturally, if you check it a second time, the probability will go down even more. So assuming that checking one's alarm clock is independent, the probably of not setting it correctly is ~ 0. And 0 is where I need it to be, because I can't stand the thought of missing school or work because I dislike sleeping and will hence sleep in a lot if given the chance. ^^;;;;;;;
I'm glad that there is statistical evidence to back up the ridiculous number of times I check my alarm clock. ;D
 Holy crow, guys, I set my alarm clock every night and check it maybe twice every blue moon, and I have slept in due to setting it wrong once in two years.
Holy crow, guys, I set my alarm clock every night and check it maybe twice every blue moon, and I have slept in due to setting it wrong once in two years.
Seriously Jay, don't sit around rationalizing your budding weirdness, just get actual professional help. Our undiagnosed obsessive extended relatives shouldn't be role models.
 Aha! But you did set it wrong once in 2 years! Which is something I don't want happening! X....D
Aha! But you did set it wrong once in 2 years! Which is something I don't want happening! X....D
@ Ally
Well... this statistical "evidence" is not really true given how the probabilities of each check is probably not independent. And the Probability of each check might be a lot lower than 0.5, so uh, less checks are probably ok. This is my mental thingummy, that I will get looked at after exams finish (else Margo will probably kill me).
 And lo, even though I was late for class, I did not get kicked out of school, nor did my grades suffer.
And lo, even though I was late for class, I did not get kicked out of school, nor did my grades suffer. 
I will kill you remotely! With my satellite of dooooom--! Which is to say, I probably won't get home until well after your exam are over, so you've got time.

 Re: Mental thingummy
Re: Mental thingummy
Math might work, although now it's sort of math + strange luck thingy; 4 is not really special to me, except from tvtropes I learned it's associated with "death" in Japan and it's a nice square number; and the only reason I check one clock 4 times in a row instead of 8 times for the other is because the 4-times-clock requires less buttons to check. I used to check it by going through the buttons until I didn't feel like I just started checking it (so basically consequently checking an alarm clock for 4 or 5 minutes straight). I sort of understand the probabilities like:
P(alarm not working with 1 check) = 0.50 for example, so assuming checks are independent (which they probably aren't) and the probability is .5 (kind of a over estimate of effects from lousy clock + human perception), then if I checked 1 clock only once, 1 out of every 2 days I would expect it not to work.
P(alarm not working with 2 checks) = 0.50^2 = 0.25 ...If I checked 1 clock twice, 1 of out of 4 days I would expect it not to work.
P(2 alarms not working with with 24 and 12 checks respectively) = 0.50^24 * 0.50^12 = 1.455 * 10 * -11 = 1.455/100,000,000,000 in about 273,972,602 years both clocks will fail once. So pretty much 0 right? The 12 and 24 checks are more by habit then by math now so hmmm...maybe I should lower the number of checks, but anyhow I am interested in your take on it.
OK, expected utility time!
"Utility" is a measure of how good/bad an outcome is. In this case, that includes whether or not you wake up at the right time, but also any other effects of checking and setting alarms - the time and effort spent checking (which you now can't use to do something else instead), annoying your sister, etc. The utility of each of these outcomes is how much you value them relative to each other (or, in the case of bad outcomes, how much you value avoiding them).
The "expected" part means how likely the outcomes are to happen. You're already doing that for the "wake up at the correct time" outcome. And it's not so relevant for the other outcomes, since checking the alarm will always take about the same amount of time, and... I'm actually not sure how frequently the checking annoys your sister, but maybe you do want to get an idea of the probability of that happening for each time you check, if that's something you value/disvalue significantly.
So to get expected utility, you multiply the probability of the outcome happening ("expected" part) by how much you value the outcome ("utility" part - this is negative if the outcome is bad). The probability weights the value of the outcome, so that the things that are most likely to happen get more attention, but unlikely things still matter.
When making a decision, you add up the expected utilities of all of the parts of the outcome that you care about, for each of the things you could decide to do. And then you do the thing that has the highest expected utility.
The expected utility for the side effects of checking your alarm (annoyance, time spent, etc.) are the same for each additional checking, because their likelihood is not affected by how many previous times you've checked. But the expected utility for waking up diminishes with each additional check, because the probability that the alarm is not already correct (and therefore the probability that the additional check will matter) goes down the more times you check. So at some point, the expected utility of the time spent etc. to check the alarm again will cancel out the expected utility of the slightly smaller chance of not waking up on time. At that point, the additional check is no longer worth it.
If you can get some data on checking alarms multiple times, it might be useful to calculate how many times you'll miss your alarm on average in a year, or in 10 years, with the alarm setups you're considering. I find that restating a number in several different ways is useful for figuring out how much to care about it. Useful for probabilities, and avoiding circular preferences in general.

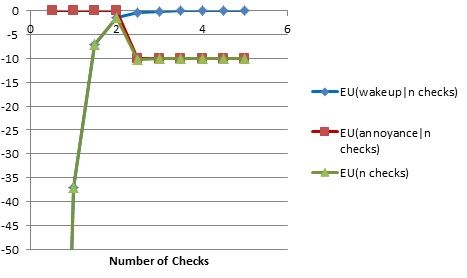
 So I managed to interpret my own graph wrong... the fact that the lines cross isn't what matters. What matters is that there's a point where "good stuff line" - "bad stuff line" (the total) starts sloping down instead of up - that is, the best number of times to check the alarm is at the peak of the blue line.
So I managed to interpret my own graph wrong... the fact that the lines cross isn't what matters. What matters is that there's a point where "good stuff line" - "bad stuff line" (the total) starts sloping down instead of up - that is, the best number of times to check the alarm is at the peak of the blue line.
My first graph isn't such a good illustration of that - it would probably mean you graphed on a scale that went up to checking the alarm at a few hundred times.
So here's another graph that zooms in on the things you'd actually consider. Probably this goes up to something like 20 or 40 alarm checkings.

 Ok. So I never did utility in my various maths classes, but I'll try to break your post down into variables and probability, which I do understand. I want that peak position of the blue curve +/- 2 for human random error.
Ok. So I never did utility in my various maths classes, but I'll try to break your post down into variables and probability, which I do understand. I want that peak position of the blue curve +/- 2 for human random error.
P(x=X) = probability of outcome occurring when variable x equals X
E(P(x=X)) = the expected probability of outcome occurring when variable x equals X
More specifically (for example):
P(x=X) = probability of "waking up at the correct time" where x is a variable and X is the number of checks I do; I want this thing so it should be positive:
E(P(x=X)) = + P(x=X)
Let's use Margo's data, because I share much of my genetic makeup and environment with her. (Since my ongoing battles with the alarm clock, I can't remember a time when it failed to wake me up.) According to Margo, she checks twice and only sleeps in once every 2 years (let's assume; obviously proper research should be more meticulously measured). I have two alarm clocks, so let's assume we can just divide the data:
P(x=2) = expected probability of waking up on time with 2 checks = (all days except 1 every 2 years) / 2 = all days except 1 every 4 years = (4 * 365 - 1) / (4 * 365) = 1459 / 1460
And E(P(x=2)) = + 1459 / 1460
Given Margo's statement on her own checks, we can assume that checking the alarm more than twice will annoy her. Generally speaking, I want to stay on good terms with my sister and not have her check me into a mental recovery ward nor kill me. Y'know. The probability of her actually doing either is probably relatively low (she hasn't done too much yet), so let us assume:
P(x> 2) = The probability of Margo getting seriously annoyed with me when the number of checks (x) exceeds 2 is 1%. She might tell you other wise.
P(x> 2) = 100%
And E(P(x > 2)) = - 1/100
Another outcome is the clocks breaking down from being over used. Naturally this affects my amount of funds, my faith in such devices, and the ability of "waking up at the correct time". I do not want this to happen. This can also happen temporarily if the power gets knocked out, but that is not something I can generally control. (Unless I buy a generator, or battery-powered alarm; unfortunately, I dislike spending money on un-fun un-essential things more than I dislike not waking up on time) This is a bit harder to guess, because over the last 1.333 year since picking up this habit, I switched to a different clock from the original one. But let use assume:
P(x >= 24) = The probability of a single clock giving out because of being checked for more than 24 times (at least) is at least 1/(1.333 * days in year) = 1/486.667; so the probability of 2 clocks:
P(x >= 24) = 2 * 1/486.667
And E(P(x >= 24)) = - 1/243.333
Ok...So...uh...I think I've missed something here.
@ Everyone who doesn't understand:
Feel free to turn ignore this post and talk about normal things like the weather or QI or something.

I don't hear my alarms. Lately it's been really bad. Sometimes, I hear it, put it on snooze a few times and them go on sleeping or if I try to wake up earlier than usual I simply do not hear it at all. To be fair, I do wake up when I need to. It seems that alarms only work when my inner clock agrees with it.
Also yay, I have a tentative schedule for the first semester! If everything goes right, I get free Fridays and finish early on Thursdays so I get mega-long weekends. Also, aikido twice a week. I was worried I wouldn't be able to fit it in. I'm happy also about the fact that one of the subjects is with the teacher I wanted, because they had been inconsistent about who was gong to give it in the timetables they'd given us before. I just hope they don't make really bad changes when we actually do start classes... there's always stuff that is wrong with the timetables they give before classes start.
 To check means (to me at least) to press a sequence of buttons to display that the alarm is on and set at a specific time. Because I'm pressing them more than normal, I have a feeling that they will wear out faster. XI
To check means (to me at least) to press a sequence of buttons to display that the alarm is on and set at a specific time. Because I'm pressing them more than normal, I have a feeling that they will wear out faster. XI
I usually do it all at once while counting the number of times to 24 or 12 and standing in front of the clock.
I usually put the alarms on different radio stations at volume levels I can hear. That way, I hear the first one first (the morning news), get sucked into the story, and the second one starts up (a pop music station) blocking the first. So I usually listen to 1 or 2 songs + news while forcing myself to get up, and walk over to turn the second radio off. The secret to not snoozing too long is putting the clock more than a few paces away from you, I think.
I remember one term I had free Fridays, but spent most of them working in group projects. :I
Here are the relevant posts (or at least most of them):

Well the consistent but minor effects are me getting headaches from being around full book shelves for more than a few hours, and checking the alarm clocks a lot before going to bed. And by a lot I mean in groups of 4 or 8....at 3 to 6 intervals. This latter effect really annoys my sister when we share the same bedroom. My extended family on both sides have their share of unusual mental thingummies and would probably be on TLC Hoarders if they didn't live in huge houses or own large amounts of land, so my immediate family just sort of let me have it, and even bought me a third alarm clock (although I only use two currently).

Yeah, It's pretty crazy. It's sort of because I learned statistics and if you check your alarm clock once, the probability of you not setting it correctly will go down. Naturally, if you check it a second time, the probability will go down even more. So assuming that checking one's alarm clock is independent, the probably of not setting it correctly is ~ 0. And 0 is where I need it to be, because I can't stand the thought of missing school or work because I dislike sleeping and will hence sleep in a lot if given the chance. ^^;;;;;;;
I like to think that I am a functioning human adult-ish people otherwise.
clemon re:alarms: Hmmm... So it's one of those L-shape graphs.

Would math help with this at all? Like... basically what's happening is either you value avoiding extremely small probabilities of setting your alarm wrong more highly than the time (and possibly annoyance) cost of checking it, or you're miscalculating expected utility of additional checking. I'll, umm... wait for you to say if you want me to explain this or not before I go into it in the interest of not being annoying |'D

Math might work, although now it's sort of math + strange luck thingy; 4 is not really special to me, except from tvtropes I learned it's associated with "death" in Japan and it's a nice square number; and the only reason I check one clock 4 times in a row instead of 8 times for the other is because the 4-times-clock requires less buttons to check. I used to check it by going through the buttons until I didn't feel like I just started checking it (so basically consequently checking an alarm clock for 4 or 5 minutes straight). I sort of understand the probabilities like:
P(alarm not working with 1 check) = 0.50 for example, so assuming checks are independent (which they probably aren't) and the probability is .5 (kind of a over estimate of effects from lousy clock + human perception), then if I checked 1 clock only once, 1 out of every 2 days I would expect it not to work.
P(alarm not working with 2 checks) = 0.50^2 = 0.25 ...If I checked 1 clock twice, 1 of out of 4 days I would expect it not to work.
P(2 alarms not working with with 24 and 12 checks respectively) = 0.50^24 * 0.50^12 = 1.455 * 10 * -11 = 1.455/100,000,000,000 in about 273,972,602 years both clocks will fail once. So pretty much 0 right? The 12 and 24 checks are more by habit then by math now so hmmm...maybe I should lower the number of checks, but anyhow I am interested in your take on it.


@ My silly problem:
Yeah, It's pretty crazy. It's sort of because I learned statistics and if you check your alarm clock once, the probability of you not setting it correctly will go down. Naturally, if you check it a second time, the probability will go down even more. So assuming that checking one's alarm clock is independent, the probably of not setting it correctly is ~ 0. And 0 is where I need it to be, because I can't stand the thought of missing school or work because I dislike sleeping and will hence sleep in a lot if given the chance. ^^;;;;;;;
I'm glad that there is statistical evidence to back up the ridiculous number of times I check my alarm clock. ;D

Seriously Jay, don't sit around rationalizing your budding weirdness, just get actual professional help. Our undiagnosed obsessive extended relatives shouldn't be role models.

@ Ally
Well... this statistical "evidence" is not really true given how the probabilities of each check is probably not independent. And the Probability of each check might be a lot lower than 0.5, so uh, less checks are probably ok. This is my mental thingummy, that I will get looked at after exams finish (else Margo will probably kill me).


I will kill you remotely! With my satellite of dooooom--! Which is to say, I probably won't get home until well after your exam are over, so you've got time.

Math might work, although now it's sort of math + strange luck thingy; 4 is not really special to me, except from tvtropes I learned it's associated with "death" in Japan and it's a nice square number; and the only reason I check one clock 4 times in a row instead of 8 times for the other is because the 4-times-clock requires less buttons to check. I used to check it by going through the buttons until I didn't feel like I just started checking it (so basically consequently checking an alarm clock for 4 or 5 minutes straight). I sort of understand the probabilities like:
P(alarm not working with 1 check) = 0.50 for example, so assuming checks are independent (which they probably aren't) and the probability is .5 (kind of a over estimate of effects from lousy clock + human perception), then if I checked 1 clock only once, 1 out of every 2 days I would expect it not to work.
P(alarm not working with 2 checks) = 0.50^2 = 0.25 ...If I checked 1 clock twice, 1 of out of 4 days I would expect it not to work.
P(2 alarms not working with with 24 and 12 checks respectively) = 0.50^24 * 0.50^12 = 1.455 * 10 * -11 = 1.455/100,000,000,000 in about 273,972,602 years both clocks will fail once. So pretty much 0 right? The 12 and 24 checks are more by habit then by math now so hmmm...maybe I should lower the number of checks, but anyhow I am interested in your take on it.
OK, expected utility time!
"Utility" is a measure of how good/bad an outcome is. In this case, that includes whether or not you wake up at the right time, but also any other effects of checking and setting alarms - the time and effort spent checking (which you now can't use to do something else instead), annoying your sister, etc. The utility of each of these outcomes is how much you value them relative to each other (or, in the case of bad outcomes, how much you value avoiding them).
The "expected" part means how likely the outcomes are to happen. You're already doing that for the "wake up at the correct time" outcome. And it's not so relevant for the other outcomes, since checking the alarm will always take about the same amount of time, and... I'm actually not sure how frequently the checking annoys your sister, but maybe you do want to get an idea of the probability of that happening for each time you check, if that's something you value/disvalue significantly.
So to get expected utility, you multiply the probability of the outcome happening ("expected" part) by how much you value the outcome ("utility" part - this is negative if the outcome is bad). The probability weights the value of the outcome, so that the things that are most likely to happen get more attention, but unlikely things still matter.
When making a decision, you add up the expected utilities of all of the parts of the outcome that you care about, for each of the things you could decide to do. And then you do the thing that has the highest expected utility.
The expected utility for the side effects of checking your alarm (annoyance, time spent, etc.) are the same for each additional checking, because their likelihood is not affected by how many previous times you've checked. But the expected utility for waking up diminishes with each additional check, because the probability that the alarm is not already correct (and therefore the probability that the additional check will matter) goes down the more times you check. So at some point, the expected utility of the time spent etc. to check the alarm again will cancel out the expected utility of the slightly smaller chance of not waking up on time. At that point, the additional check is no longer worth it.
If you can get some data on checking alarms multiple times, it might be useful to calculate how many times you'll miss your alarm on average in a year, or in 10 years, with the alarm setups you're considering. I find that restating a number in several different ways is useful for figuring out how much to care about it. Useful for probabilities, and avoiding circular preferences in general.
My first graph isn't such a good illustration of that - it would probably mean you graphed on a scale that went up to checking the alarm at a few hundred times.
So here's another graph that zooms in on the things you'd actually consider. Probably this goes up to something like 20 or 40 alarm checkings.

P(x=X) = probability of outcome occurring when variable x equals X
E(P(x=X)) = the expected probability of outcome occurring when variable x equals X
More specifically (for example):
P(x=X) = probability of "waking up at the correct time" where x is a variable and X is the number of checks I do; I want this thing so it should be positive:
E(P(x=X)) = + P(x=X)
Let's use Margo's data, because I share much of my genetic makeup and environment with her. (Since my ongoing battles with the alarm clock, I can't remember a time when it failed to wake me up.) According to Margo, she checks twice and only sleeps in once every 2 years (let's assume; obviously proper research should be more meticulously measured). I have two alarm clocks, so let's assume we can just divide the data:
P(x=2) = expected probability of waking up on time with 2 checks = (all days except 1 every 2 years) / 2 = all days except 1 every 4 years = (4 * 365 - 1) / (4 * 365) = 1459 / 1460
And E(P(x=2)) = + 1459 / 1460
Given Margo's statement on her own checks, we can assume that checking the alarm more than twice will annoy her. Generally speaking, I want to stay on good terms with my sister and not have her check me into a mental recovery ward nor kill me. Y'know. The probability of her actually doing either is probably relatively low (she hasn't done too much yet), so let us assume:
P(x> 2) = The probability of Margo getting seriously annoyed with me when the number of checks (x) exceeds 2 is 1%. She might tell you other wise.
P(x> 2) = 100%
And E(P(x > 2)) = - 1/100
Another outcome is the clocks breaking down from being over used. Naturally this affects my amount of funds, my faith in such devices, and the ability of "waking up at the correct time". I do not want this to happen. This can also happen temporarily if the power gets knocked out, but that is not something I can generally control. (Unless I buy a generator, or battery-powered alarm; unfortunately, I dislike spending money on un-fun un-essential things more than I dislike not waking up on time) This is a bit harder to guess, because over the last 1.333 year since picking up this habit, I switched to a different clock from the original one. But let use assume:
P(x >= 24) = The probability of a single clock giving out because of being checked for more than 24 times (at least) is at least 1/(1.333 * days in year) = 1/486.667; so the probability of 2 clocks:
P(x >= 24) = 2 * 1/486.667
And E(P(x >= 24)) = - 1/243.333
Ok...So...uh...I think I've missed something here.
@ Everyone who doesn't understand:
Feel free to turn ignore this post and talk about normal things like the weather or QI or something.
Mar 5, 2013 1:34:10 GMT Soff said:
The only thing that confuses me in all this (or that it worries me not to understand though I think I got the gist of the stuff you're doing, even if I could not do it myself...) is what does it mean to "check" the alarms? It means that you wake up, turn on the light and look at clocks? Because that is what assumed, but I do not understand how that make the clocks give out, so I'm guessing that I'm not understanding something.I don't hear my alarms. Lately it's been really bad. Sometimes, I hear it, put it on snooze a few times and them go on sleeping or if I try to wake up earlier than usual I simply do not hear it at all. To be fair, I do wake up when I need to. It seems that alarms only work when my inner clock agrees with it.
Also yay, I have a tentative schedule for the first semester! If everything goes right, I get free Fridays and finish early on Thursdays so I get mega-long weekends. Also, aikido twice a week. I was worried I wouldn't be able to fit it in. I'm happy also about the fact that one of the subjects is with the teacher I wanted, because they had been inconsistent about who was gong to give it in the timetables they'd given us before. I just hope they don't make really bad changes when we actually do start classes... there's always stuff that is wrong with the timetables they give before classes start.

I usually do it all at once while counting the number of times to 24 or 12 and standing in front of the clock.
I usually put the alarms on different radio stations at volume levels I can hear. That way, I hear the first one first (the morning news), get sucked into the story, and the second one starts up (a pop music station) blocking the first. So I usually listen to 1 or 2 songs + news while forcing myself to get up, and walk over to turn the second radio off. The secret to not snoozing too long is putting the clock more than a few paces away from you, I think.
I remember one term I had free Fridays, but spent most of them working in group projects. :I

 )
)